Getting Volk into GNU Radio
We've been talking about integrating
Volk into GNU Radio for what seems like forever. So what took us so damn long? Well, it's coming, very shortly, and I wanted to take a moment to discuss both the issues of Volk in GNU Radio and how to make use of it with some brand-new additions.
The main problem with using Volk in GNU Radio is the alignment requirements of most
SIMD systems. In many SIMD architectures, Intel most notably (and we'll stick with them in these examples as it's what I'm most familiar with), we have a byte-alignment requirement when loading data into the SIMD-specific registers. When moving data in and out, there is a concept of aligned and unaligned loads and stores. You take a hit when using the unaligned versions, though, and they are not desirable. In SSE code, we need to by 16-byte aligned while the newer AVX architecture wants a 32-byte alignment.
But we have the dynamic scheduler in GNU Radio that moves data between blocks in chunks of items (where an item is whatever you want: floats, complex floats, samples, etc.). The scheduler tries to maximize system throughput by moving as large a chunk as possible to give the work function lots of data to crunch at once. Larger chunks minimize the overhead of going into the scheduler to get more data. But because we are never sure how much data any one block has ready for the next in the chain of GNU Radio blocks, we cannot always guarantee the number of items available, and so we cannot guarantee a specific byte alignment of our data streams.
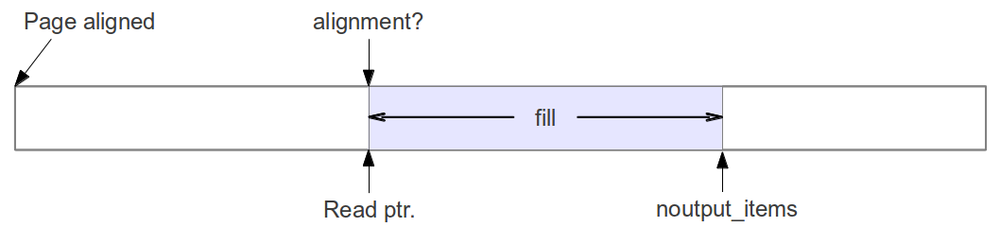
We have one thing going for us, though: all buffers are page-aligned at the start. This is great since a page alignment is good enough for any current or foreseeable SIMD alignment requirement (16 or 32 bytes right now, and when we get to the problem of requiring more than 4k alignments, I'll be happy enough to readdress the problem then). So the first call to work on a buffer is always aligned.
But what if the work function is called with a number of items that breaks the alignment? What are we supposed to do then?
The first attempt at a solution was to use the concept of setting a set_output_multiple value for the block. This call tells the scheduler that the block can only handle chunks of data that contain a number of items that is a multiple of this value. So if we have floats in SSE chips, we need a multiple of 4 floats per call to the work function. It will never be called with less than 4 or some odd number that will ruin our alignment.
But there's a problem with that approach. The scheduler doesn't really function well when given that restriction. Specifically, there are two issues. First, if the data stream being processed is finite and that number is not a multiple of what's required by the alignment, then the last number of items won't ever be processed. That's not the biggest deal in the world as GNU Radio is typically meant to stream data, but it could be a problem for many applications of processing data from a file.
The second problem, though, is latency. When processing packetized data, we cannot produce a packet until we have enough samples to make the packet. But at some point, we have the last few samples sitting in the buffer waiting to be processed. Because of our output multiple restriction, we leave those sitting behind until more samples are available so that the scheduler can pass them on. That would mean a fairly large amount of added latency to handle a packet, and that's unacceptable.
No, what we need is a solution that keeps the data flowing as best as it can while still working towards keeping the buffers aligned.
Branch Location
This post discusses issues that will hopefully be merged into the main source code of GNU Radio soon. However, I would like it to undergo significant testing, first, and so have only published a branch at:
http:github.com/trondeau/gnuradio.git
as the branch safe_align.
Scheduler Alignment
Instead of using the set_output_multiple approach, we need a solution that meets the following goals:
- Minimize effect to latency; maximize throughput.
- Try to maintain alignment of buffers whenever possible.
- When not possible to keep alignment, pass on data quickly.
- minimize latency accrued by holding data.
- Re-establish alignment but not at the expense of extra calls.
- pass on the largest buffer possible that re-establishes alignment.
- don't pass the minimum required. The extra overhead of calling a purposefully-truncated work function is greater than the benefit of realigning quickly.
In it's implementation, we want to minimize any added computation to the scheduler and slow down our code.
In the approach that we came up with, the scheduler looks at the number of items it has available for the block. If there are enough items to keep the buffers aligned, it passes on the largest number of samples possible that maintains the alignment. If there aren't enough, then it sends them along anyway, but it sets a flag that tells the block of the alignment problem.
When the buffers are misaligned, the scheduler must try to correct the alignment. There are two ways of doing this. The easiest way is just to pass on the minimum number of items possible that re-establishes alignment. The problem with this approach is that the number is really small, so you are asking the work function to handle 1, 2, or 3 items, say. Then it has to go back to the scheduler and ask for more. This kind of behavior incurs a tremendous amount of overhead in that it deals more with moving the data than processing it.
The second way of handling the unalignment is to take the amount of data currently available and pass on the largest possible chunk of items that will re-establish the alignment. This forces us to handle another call to work with unaligned data, but the penalty for doing that is much less than the overhead of purposefully handling small buffers. In my experiments and analysis, most of the data comes across aligned, anyway, so these calls are minimal.
To accomplish these new rules, the GNU Radio gr_block class (which is a parent class to all blocks) has these new functions:
void set_alignment (int multiple);
int alignment () const { return d_output_multiple; }
void set_unaligned (int na);
int unaligned () const { return d_unaligned; }
void set_is_unaligned (bool u);
bool is_unaligned () const { return d_is_unaligned; }
A block's work function can check it's alignment and make the proper decision on what to do based on that information. The block can test the is_unaligned() and call. If it indicates that the buffers are aligned, than the aligned Volk kernel can be called. Otherwise, it can either process the data directly or call an unaligned kernel.
In order not to make this blog post longer than it already is, I will post a separate blog post discussing the method and results of benchmarking all of this work. In it, just to tease, I'll be showing a few surprising results. First, I'll show that the use of Volk can give us dramatic improvements for a lot of simple blocks (ok, that's not surprising). Second, on the tested processors, I see almost no penalty for making unaligned loads and stores. And third, lest you think that last claim makes all of this work unnecessary, my test show that the efforts to keep the alignment going in the new scheduler actually improves the processing speed even without using Volk. So there is a two-fold benefit to this work: one from the scheduler itself and then a second effect of Volk.
Making Unaligned Kernels
Because we will be processing unaligned buffers in this approach, we need to either handle these cases with generic implementations or use an unaligned kernel. The generic version of the code would be like what is already in a block now that we would like to transition to using Volk. This would be the standard C/C++ for-loop math.
A useful approach, though, is to make use of unaligned Volk kernel. Even though an unaligned load is a bit more costly than an aligned call, we try to maximize the size of the buffers to process and the overall affect is still faster than a generic for loop. So it behooves us to call the unaligned version in these cases, which might mean making a new kernel specifically for this.
Luckily, in most cases, the only difference between an aligned Volk kernel and an unaligned one is the use of loadu instead of load and storeu instead of store. These two simple differences makes it really easy to create an unaligned kernel.
With this approach, a GNU Radio block can look really simple. Let's use the gr_multiply_cc block as an example. Here's the old version of the call:
int
gr_multiply_cc::work (int noutput_items,
gr_vector_const_void_star &input_items,
gr_vector_void_star &output_items)
{
gr_complex *optr = (gr_complex *) output_items[0];
int ninputs = input_items.size ();
for (size_t i = 0; i < noutput_items*d_vlen; i++){
gr_complex acc = ((gr_complex *) input_items[0])[i];
for (int j = 1; j < ninputs; j++)
acc *= ((gr_complex *) input_items[j])[i];
*optr++ = (gr_complex) acc;
}
return noutput_items;
}
That version uses a for-loop over both he number of inputs and number of items. Here's what it looks like when we call Volk.
int
gr_multiply_cc::work (int noutput_items,
gr_vector_const_void_star &input_items,
gr_vector_void_star &output_items)
{
gr_complex *out = (gr_complex *) output_items[0];
int noi = d_vlen*noutput_items;
memcpy(out, input_items[0], noi*sizeof(gr_complex));
if(is_unaligned()) {
for(size_t i = 1; i < input_items.size(); i++)
volk_32fc_x2_multiply_32fc_u(out, out, (gr_complex*)input_items[i], noi);
}
else {
for(size_t i = 1; i < input_items.size(); i++)
volk_32fc_x2_multiply_32fc_a(out, out, (gr_complex*)input_items[i], noi);
}
return noutput_items;
}
Here, we only loop over each input, but the calls themselves are to the Volk multiply complex kernel. We test the unaligned flag first. If the buffers are flagged as unaligned, we use the volk_32fc_x2_multiply_32fc_u kernel where the final "u" indicates that this is an unaligned kernel. So for each input stream, we process the data this way. In particular, this kernel only takes in two streams at once to multiply together, so we take the output and multiply it by the next input stream after having first pre-loaded the output buffer with the first input stream.
Now, if the block's buffers are aligned, the flag will indicate as much and the aligned version of the kernel is called. Notice that the only difference between the kernels is the "a" at the end instead of the "u" to indicate that this is an aligned kernel.
If we didn't have an unaligned kernel available, we could either create one or just call the old version of the gr_multiply_cc's work function in this case.
Blocks Converted so Far
These next few sections are starting to get really low-level and specific, so feel free to stop reading unless you are really interested in the development work. I include this as much for the historical reference as anything.
Most of these blocks that I have so far moved over to using Volk fall into the category of the "low-hanging fruit." That means that, mostly, the Volk kernels existed or were easy to create from existing Volk kernels (such as making unaligned versions of them), that the block only needed a single Volk kernel to perform the activity required, and that had very straight-forward input to output relationships.
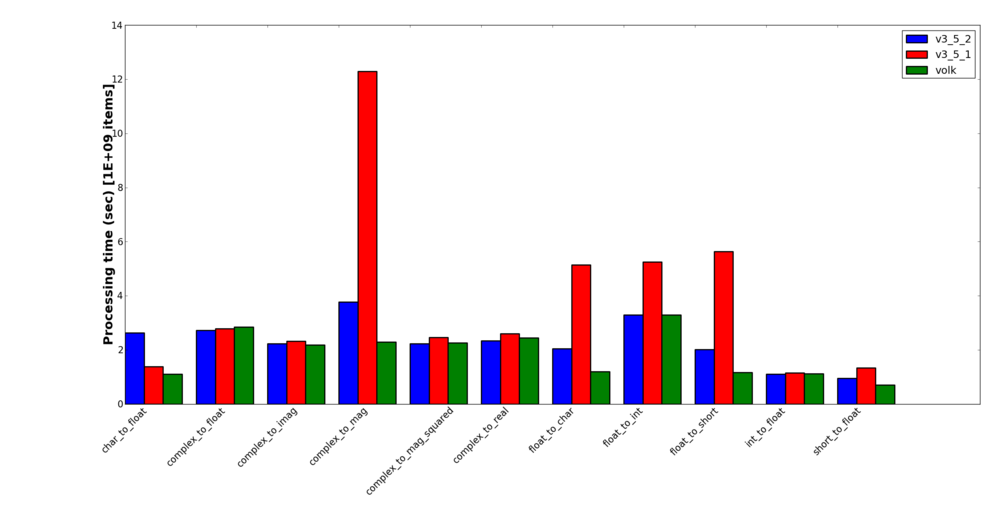
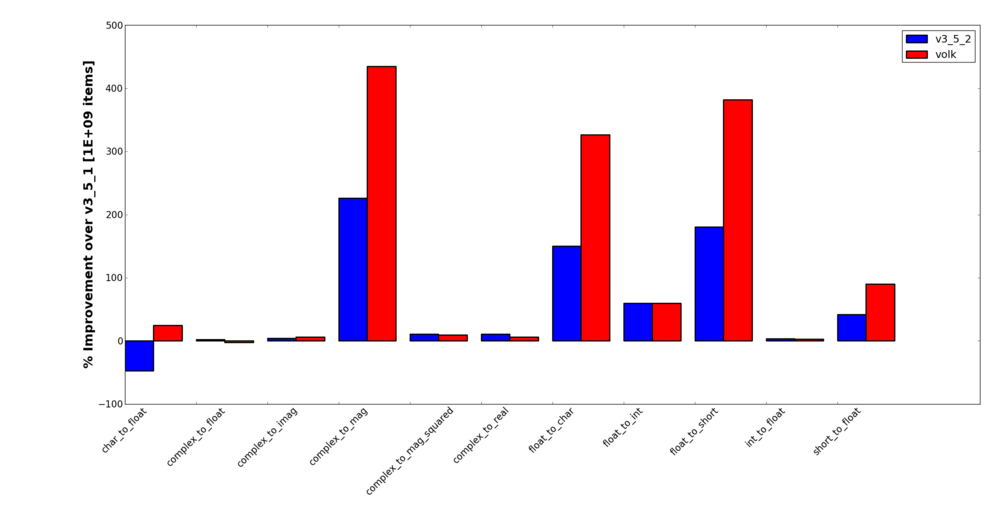
On occasion, I went and added a few things that I thought were useful. The char->short and short->char type conversions did not exist, but they were already a Volk kernel, so making them a GNU Radio block was easy and, hopefully, useful.
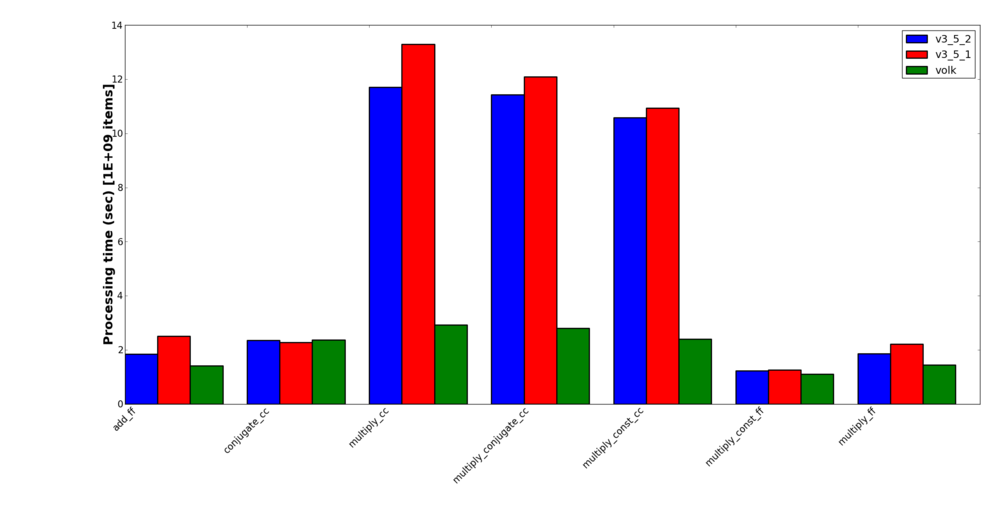
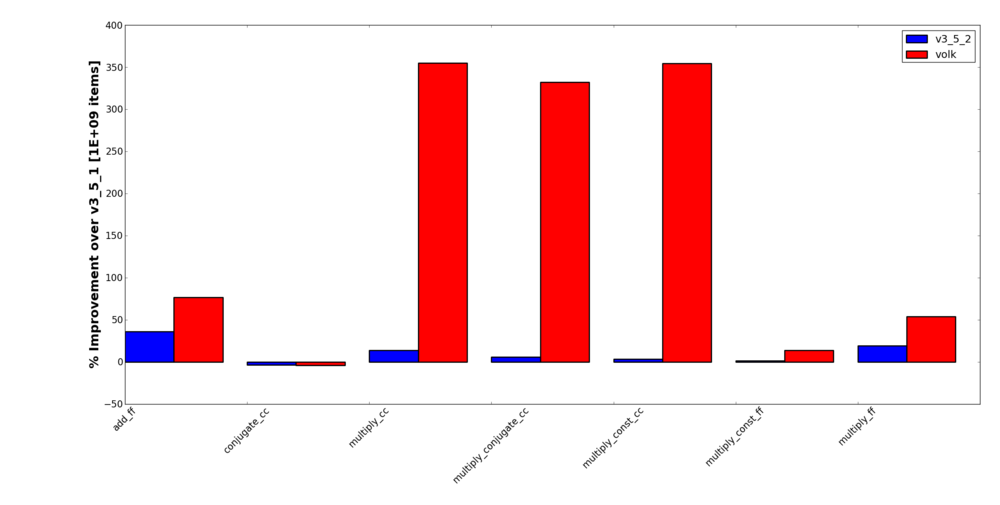
I also added a gr_multiply_conjugate_cc block. This one made a lot of sense to me. First, it was really easy to add the two lines it took to convert the Volk kernel that did a complex multiply into the conjugate and multiply kernel that's there now. Since this is such an often-used function in DSP, it just seemed to make sense to have a block that did it. My benchmarking shows a notable improvement in speed by combining this operation into a single block, too. Just to note, this block takes in two (and only two) inputs where the second stream is the one that gets conjugated.
What follows is a list of blocks o different types convered to using Volk
Type conversion blocks
- gnuradio-core/src/lib/general/gr_char_to_float
- gnuradio-core/src/lib/general/gr_char_to_short
- gnuradio-core/src/lib/general/gr_complex_to_xxx
- gnuradio-core/src/lib/general/gr_float_to_char
- gnuradio-core/src/lib/general/gr_float_to_int
- gnuradio-core/src/lib/general/gr_float_to_short
- gnuradio-core/src/lib/general/gr_int_to_float
- gnuradio-core/src/lib/general/gr_short_to_char
- gnuradio-core/src/lib/general/gr_short_to_float
Filtering blocks
- gnuradio-core/src/lib/filter/gr_fft_filter_ccc
- gnuradio-core/src/lib/filter/gr_fft_filter_fff
- gnuradio-core/src/lib/filter/gri_fft_filter_ccc_generic
- gnuradio-core/src/lib/filter/gri_fft_filter_fff_generic
General math blocks
- gnuradio-core/src/lib/general/gr_add_ff
- gnuradio-core/src/lib/general/gr_conjugate_cc
- gnuradio-core/src/lib/general/gr_multiply_cc
- gnuradio-core/src/lib/general/gr_multiply_conjugate_cc
- gnuradio-core/src/lib/general/gr_multiply_const_cc
- gnuradio-core/src/lib/general/gr_multiply_conjugate_cc
- gnuradio-core/src/lib/general/gr_multiply_const_cc
- gnuradio-core/src/lib/general/gr_multiply_const_ff
- gnuradio-core/src/lib/general/gr_multiply_ff
Gengen to General
One thing that might confuse people who have previously developed in the guts of GNU Radio is how I moved some of the blocks from gengen to general. Many GNU Radio blocks perform some function, like basic mathematical operations on two or more streams, that behave identically from a code standpoint but which use different data types. These have been put into the gengen directory as templated files where a Python script is used to autogenerate the type-specific class. This was before Swig would properly handle actual C++ templates, so we were left doing it this way.
Well, with Volk, we don't really have the option to template classessince the Volk call is highly specific to the data type used. So when moving certain math block for a specific type out of gengen, we went with the simple solution of removing that data type from the autogeneration scripts and placing it into general as a stand-alone block that can call the right Volk function. Good examples are the gr_multiply_cc and gr_multiply_ff blocks to see what I mean.
This really seems like the simplest possible answer to the problem. It maintains our block structure that we've been using for almost a decade now and keeps things clean and simple for both developers and users. The downside is some duplication of code, but with the Volk C functions, that is somewhat inevitable and not a huge issue to deal with.
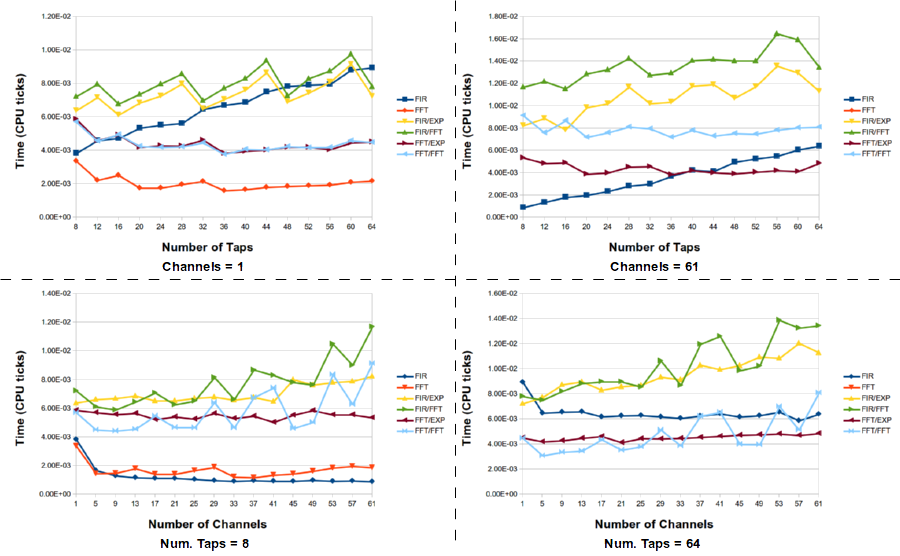
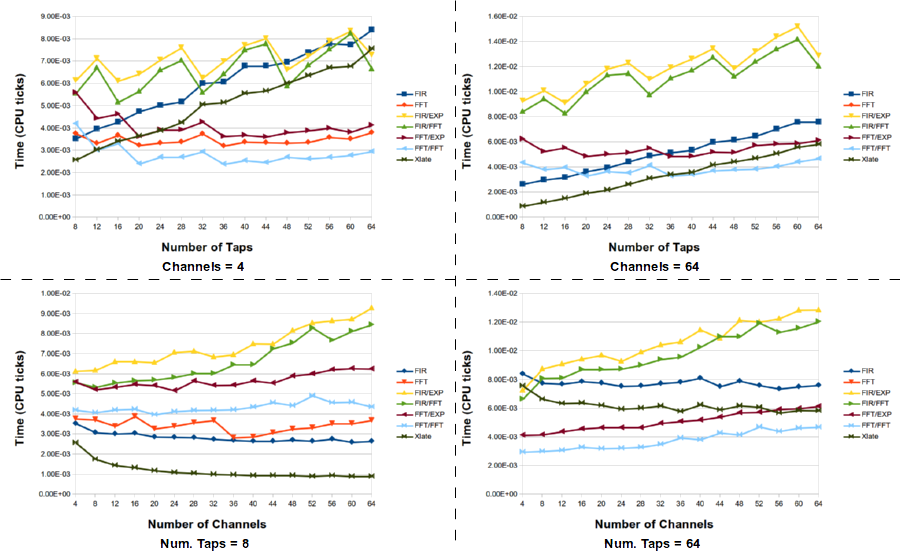What this tells us is that the standard method of down shifting a signal and filtering it is not the optimal choice. However, the best selection of filter technique really depends on the number of channels (e.g., the decimation factor) and the number of taps in the filter. For large channels and taps, the FFT/FFT version of the PFB decimating filter is the best here, but there are times when the frequency xlating filter is really the best choice. Here is the full data set for the channelizing experiments.
