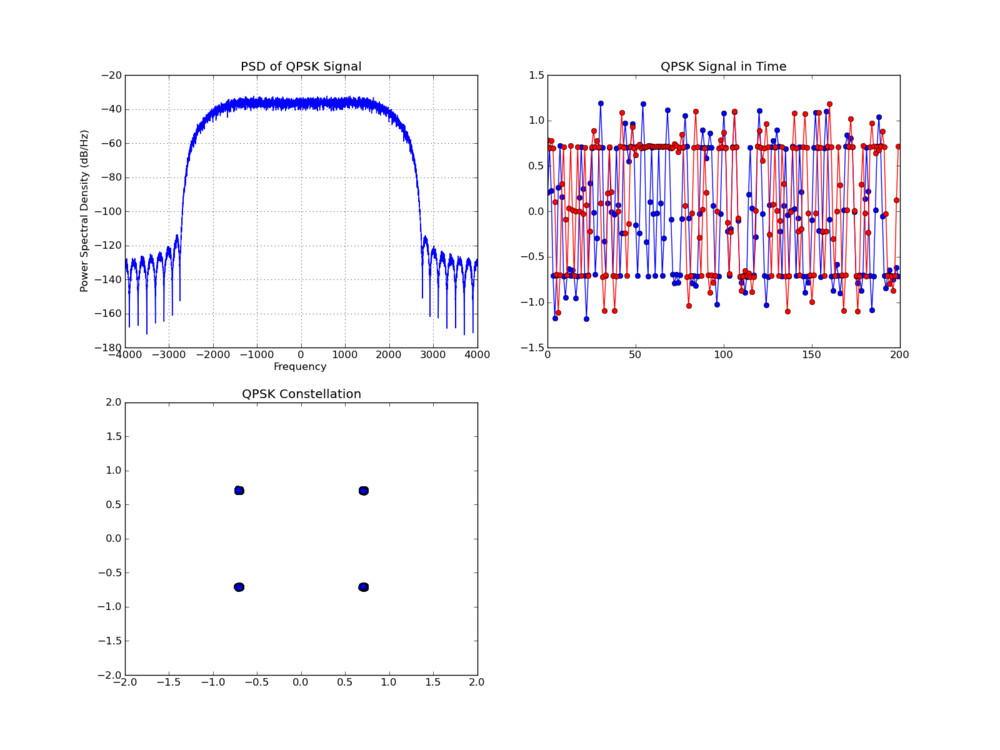
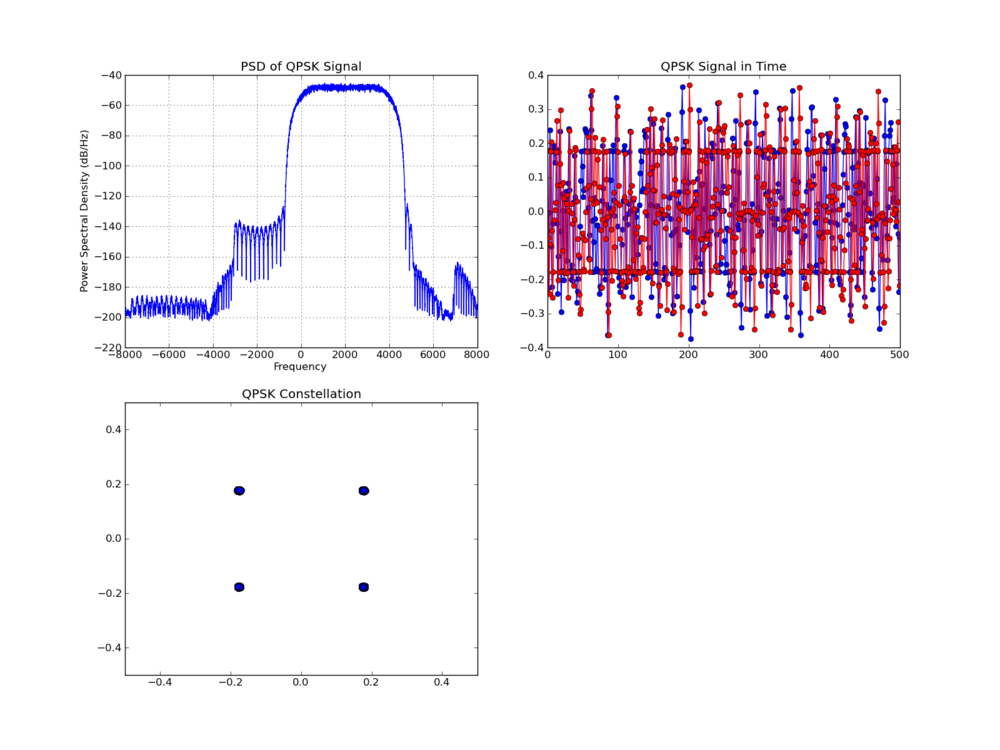
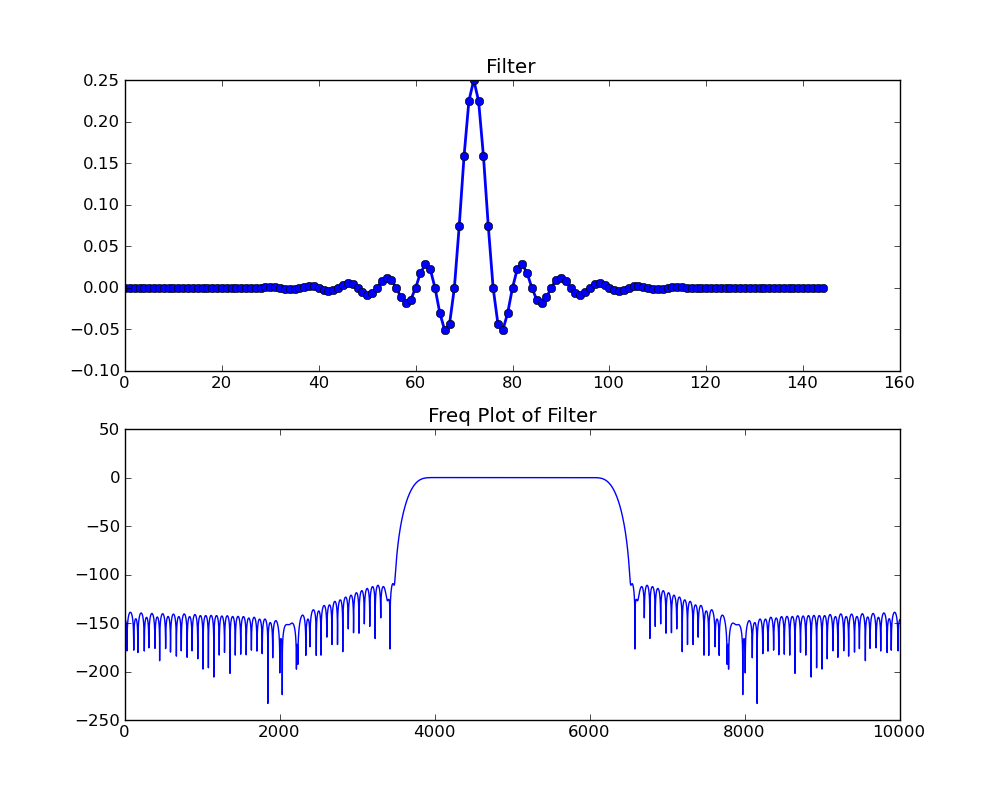
I've talked in various presentations about the merits of fast convolution, which we implement in GNU Radio as the fft_filter. When you have enough taps in your filter, and this is architecture dependent, it is computationally cheaper to use the fft_filter over the normal fir_filters. The cross-over point tends to be somewhere between 10 and 30 taps depending on your machine. On my AVX-enabled system, it's down around 10 taps.
However, Sylvain Munaut pointed out decreasing performance of the FFT filters over normal FIR filters when decimating a high rates. The cause was pretty obvious. In the FIR filter, we use a polyphase implementation where we downsample the input before filtering. However, in the FFT filter's overlap-and-save algorithm, we filter the input first and then downsample on the output, which means we're always running the FFT filter at full rate regardless of how much or little data we're actually getting out of it.
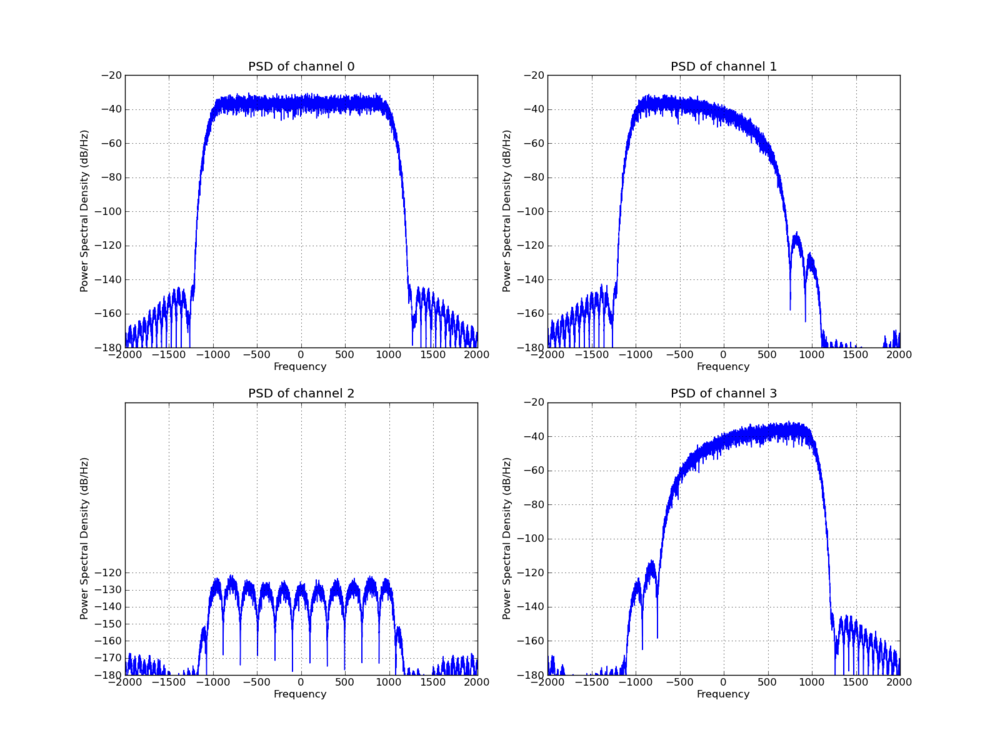
GNU Radio also has a pfb_decimator block that works as a down-sampling filter and also does channel selection. Like the FIR filter, this uses the concept of polyphase filtering and has the same efficiencies from that perspective. The difference is that the FIR filter will only give you the baseband channel out while this PFB filter allows us to select any one of the Nyquist zone channels to extract. It does so by multiplying each arm of the filterbank by a complex exponential that constructively sums all of the aliases from our desired channel together while destructively cancelling the rest.
After the discussion about the FIR vs. FFT implementation, I went into the guts of the PFB decimating filter to work on two things. First, the internal filters in the filterbank could be done using either normal FIR filter kernels or FFT filter kernels. Likewise, the complex exponential rotation can be realized by simply multiplying each channel with a complex number and summing the results, or it could be accomplished using an FFT. I wanted to know which implementations were better.
Typically with these things, like the cross-over point in the number of taps between a FIR and FFT filter, there are going to be certain situations where different methods perform better. So I outfitted the PFB decimating filter with the ability to select which fitler and which rotation structures to use. You pass these in as flags to the constructor of the block as:
- False, False: FIR filters with complex exponential rotation
- True, False: FIR filters with the FFT rotator
- False, True: FFT filters with the exponential rotator
- True, True: FFT filters with the FFT rotator
This means we get to pick the best combination of methods depending on whatever influences we might have on how each performs. Typically, given an architecture, we'll have to play with this to understand the trade-offs based on the amount of decimation and size of the filters.
I created a script that uses our Performance Counters to give us the total time spent in the work function of each of these filters given the same input data and taps. It runs through a large number of situations for different number of channels (or decimation) and different number of taps per channel (the total filter size is really the taps len times the number of channels). Here I'll show just a handful of results to give an idea what the trade-off space looks like for the given processor I tested on (Intel i7-2620M @ 2.7 GHz, dual core with hyper threading; 8 GB DDR3 RAM). This used GNU Radio 3.7.3 (not released, yet) with GCC 4.8.1 using the build type RelWithDebInfo (release mode for full optimization that also includes debug symbols).
Here are a few select graphs from the data I collected for various numbers of channels and filter sizes. Note that the FFT filter is not always represented. For some reason that I haven't nailed down, yet, the timing information for the FFT filters was bogus for large filters, so I removed it entirely. Yet, I was able to independently test the FFT filters for different situations like those here and they performed fine; not sure why the timing was failing in these tests.
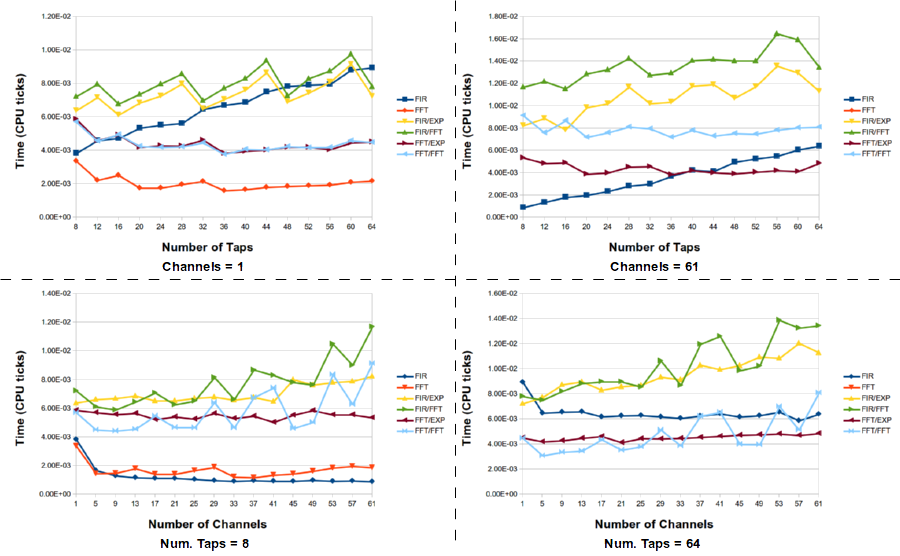
We see that the FIR filters and FFT filters almost always win out, but they are doing far fewer operations. The PFB decimator is going through the rotation stage, so of course it will never be as fast as the normal FIR filter. But within the space of the PFB decimating filters, we see that generally the FFT filter version is better while the selection between the exponential rotator and FFT rotator is not as clear-cut. Sometimes one is better than the other, which I am assuming is due to different performance levels of the FFT for a given number of channels. You can see the full data set here in OpenOffice format.
Filtering and Channelizing
A second script looks at a more interesting scenario where the PFB decimator might be useful over the FIR filter. Here, instead of just taking the baseband channel, we use the ability of the PFB decimator to select any given channel. To duplicate this result, the input to the FIR filter must first be shifted in frequency to baseband the correct channel and then filtered. To do this, we add a signal generator and complex multiply block to handle the frequency shift, so the resulting time value displayed here is the sum of the time spent in each of those blocks. The same is true for the FFT filters.
Finally, we add another block to the experiment. We have a freq_xlating_fir_filter that does the frequency translation, filtering, and decimation all in one block. So we can compare all these methods to see how each stacks up.
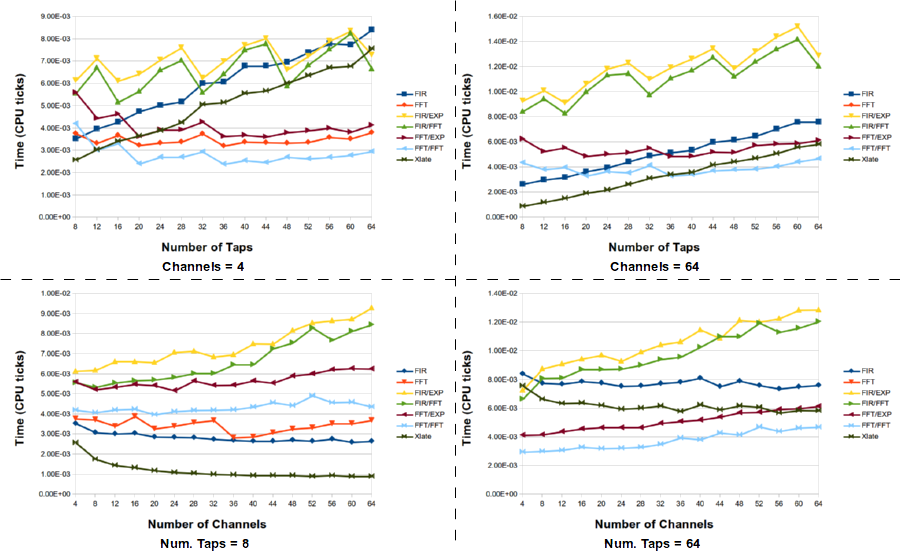 What this tells us is that the standard method of down shifting a signal and filtering it is not the optimal choice. However, the best selection of filter technique really depends on the number of channels (e.g., the decimation factor) and the number of taps in the filter. For large channels and taps, the FFT/FFT version of the PFB decimating filter is the best here, but there are times when the frequency xlating filter is really the best choice. Here is the full data set for the channelizing experiments.
What this tells us is that the standard method of down shifting a signal and filtering it is not the optimal choice. However, the best selection of filter technique really depends on the number of channels (e.g., the decimation factor) and the number of taps in the filter. For large channels and taps, the FFT/FFT version of the PFB decimating filter is the best here, but there are times when the frequency xlating filter is really the best choice. Here is the full data set for the channelizing experiments.
One question that came to mind after collecting the data and looking at it is what optimizations FFTW might have in it. I know it does a lot of SIMD optimization, but I also remember a time when the default binary install (via Ubuntu apt-get) did not take advantage of AVX processors. Instead, I would have to recompile FFTW with AVX turned on, which might also make a difference since many of the blocks in GNU Radio use VOLK for SIMD optimization, including AVX that my processor supports. That might change things somewhat. But the important thing to look at here are not absolute numbers but general trends and trying to get a feeling for what's the best for your given scenario and hardware. Because these can change, I provided the scripts in this post so that anyone else can use them to experiment with, too.