Benchmarking Volk in GNU Radio
The intention of Volk is to increase the speed of our signal processing capabilities in GNU Radio, and so there needs to be a way to look at this. In particular, there were some under-the-hood changes to the scheduler to allow us to more efficiently use Volk (by trying to provide only aligned Volk call; see Volk Integration to GNU Radio for more on that). These changes ended up putting more lines of code into the scheduler so that every time a block's work function is called, the scheduler has more computations and logic to perform.
Because of these changes, I am interested in understanding the performance hit taken by the change in the scheduler as well as the performance gain we would get from using Volk. If the hit to the scheduler is less than a few percentage points while the gain from Volk is much larger, then we win.
Performance Measuring
There is a lot of debate about what the right performance measurement is for something like this. In signal processing algorithms, we are interested in looking at the speed that it can process a sample (or bit, symbol, etc.), so a time-based measurement is what we are going to look at. Specifically, how much time does it take a block to process $N$ number of samples?
If we are interested in timing a block, the next question is to ask what clock to use? And if we look into this, everyone has their own opinion on it. There's wall time, but that's suspect because it doesn't account for interruptions by the OS. There's the user and system times, but they don't seem to really represent the time it actually takes a program to produce the output; and do we combine those times or just use one of them? This also really represents a lower bound if no sharing were occurring and with no other system overhead.
In the end, I decided what I cared about, and what our users would care about, is the expected time taken by a block to run. So I'm going with the wall clock method here. Then there's the question of mean, min, or max time? They all represent different ways to look at the results. It is, frankly, easy enough to capture all three measurements and let you decided later which is important (for that matte, it would be an easy edit to the benchmark tools to also collect the user and system time for those who want that info, too).
The results shown in this post simply represent the mean of the wall time for a certain number of iterations for processing a certain number of samples for each block. I am also going to show the results from only one machine here to keep this post relatively short.
Measurement Tools
I built a few measurement tools to both help me keep track of things and allow anyone else who wants to test their system's performance to do so easily. These tools are located in gnuradio- examples/python/volk_benchmark. It includes two Python programs for collecting the data and a plotting program to display the data in different ways. I won't repost here the details of how to use them. There's a lengthy and hopefully complete README in the directory to describe their use.
Measurement Results
For these measurements, I have two data collection programs: volk_math.py and volk_types.py. The first one runs through all of the math functions that were converted to using Volk and the second runs through all of the type conversions that were 'Volkified.' These could have easily been done as one program, but it makes a bit of logical sense to separate them.
The system I ran these tests on is an Intel quad-core i7 870 (first gen) at 2.93 GHz with 8 GB of DDR3 RAM. It has support for these SIMD architectures: sse sse2 ssse3 sse4_1 sse4_2.
I'm interested in comparing the results of three cases. The first case is the 'control' experiment, which is the 3.5.1 version of GNU Radio which has no edits to the scheduler or the use of Volk. Next, I want to look at the scheduler with the edits but still no Volk, which I will refer to as the 3.5.2 version of GNU Radio. The 'volk' case is the 3.5.2 version that uses Volk for the tests.
The easiest way to handle these cases was to have two parallel installs, one for version 3.5.1 and the other for 3.5.2. To test the Volk and non-Volk version of 3.5.2, I simply edited the ~/.volk/volk_config file and switch all kernels to use the 'generic' version (see the README file in the volk_benchmark directory for more details on this).
For the results shown below, click on the image for an enlarged version of the graph.
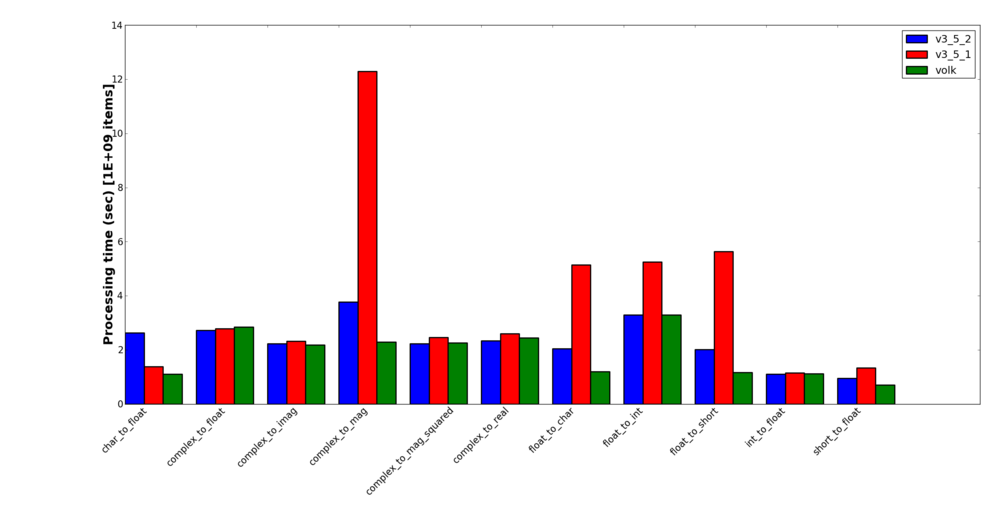
Looking at the type conversion blocks, we get the following graph:
Another way to look at the results is to look at the percent speed difference between the 3.5.2 versions and the 3.5.1. So this graph shows us how much increase (positive) or decrease (negative) of speed the two cases have over the 3.5.1 control case.
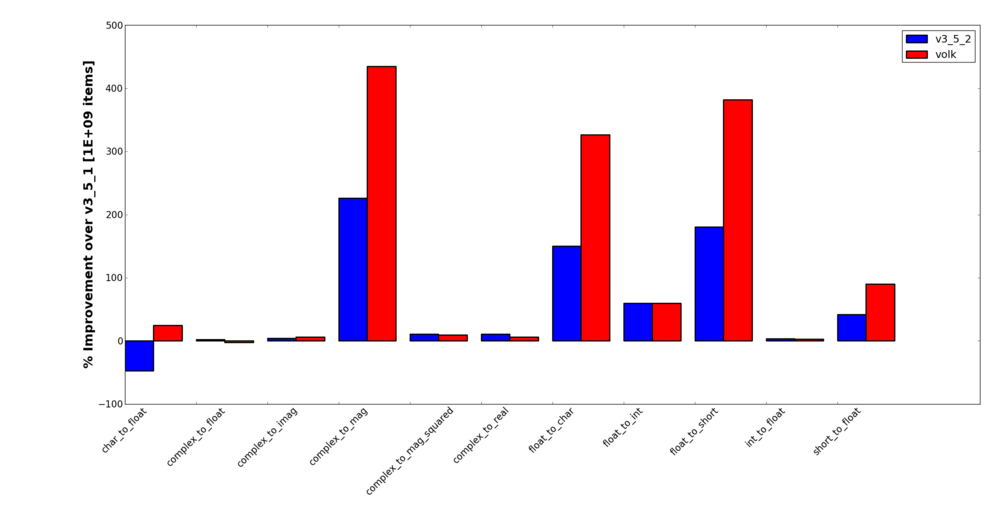 Percent Improvement Over v3.5.1 for Type Conversion Blocks
Percent Improvement Over v3.5.1 for Type Conversion Blocks
These are the same graphs for the math kernels.
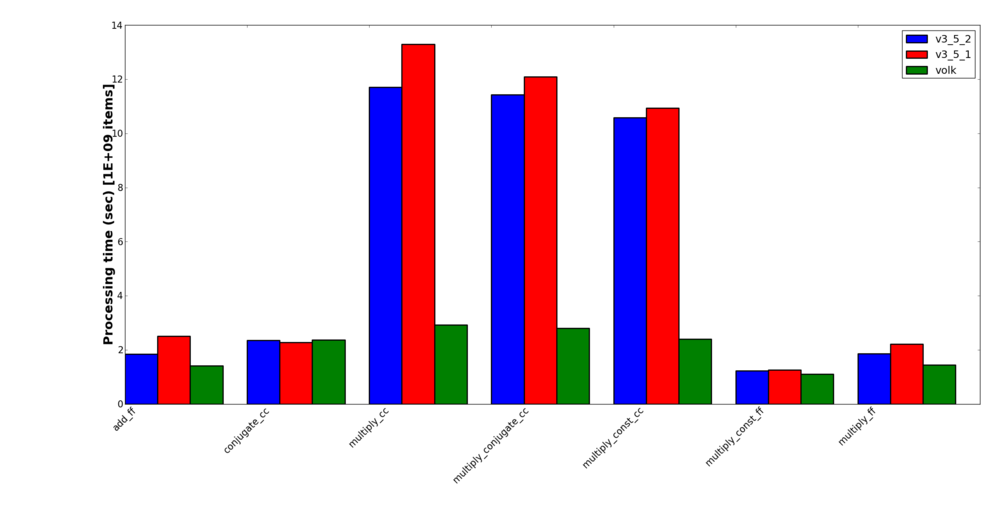 Volk Math Results
Volk Math Results
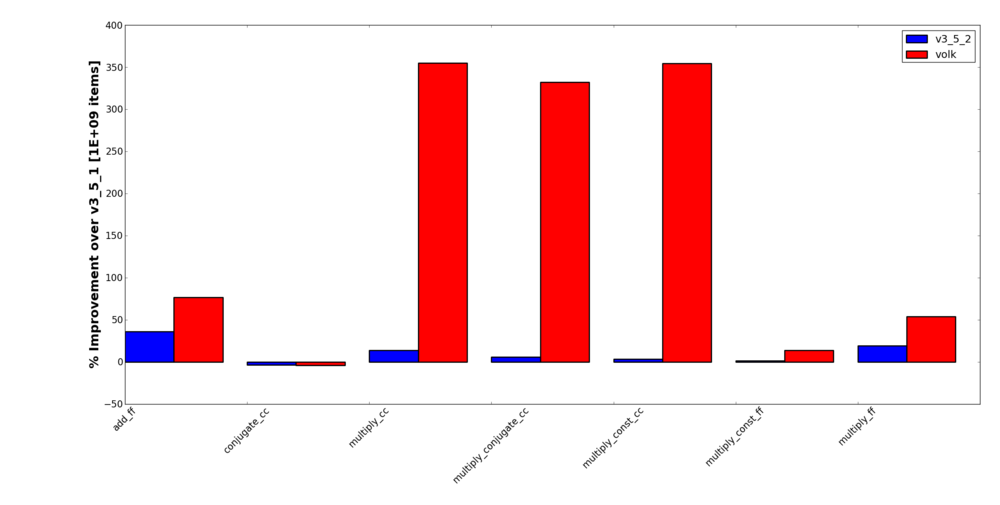 Percent Improvement Over v3.5.1 for Math Blocks
Percent Improvement Over v3.5.1 for Math Blocks
There are two interesting trends here. The most uninteresting one is that Volk generally provides a massive improvement in the speed of the blocks, the more complicated the block (like complex multiplies) the more we gain from using Volk.
The first really interesting result is the improvement in speed between the schedulers from 3.5.1 and 3.5.2. As I mentioned earlier, we increased the number of lines of code in the scheduler that make calculations and logic and branching calls. I expected us to do worse because of this. My conjecture here is that by providing mostly aligned blocks of memory, there is something happening with data movement and/or the cache lines that is improved. So simply aligning the data (as much as possible) is a win even without Volk.
The other area this interesting is that in the rare case, the Volk call comes out to be worse than the generic and/or the v3.5.1 version of the block. The only math call where this happens is with the conjugate block. I can only assume that conjugating a complex number is so trivial (the sign flip of the imaginary part) that the code for it is highly optimize already. We are, though, talking about less than 5% hit on the performance, though. On the other hand, the multiply conjugate block, which is mostly when the conjugate is used in signal processing, is around 350% faster.
The complex to float conversion is a bit more of a head scratcher. Again, though, we are talking about a minor (< 3%) difference. But stiil, that these do not perform better is really interesting. Hopefully, we can analyze this farther and come up with some conclusions as to why this is occuring and maybe even improve the performance more.
Just a note that as of 3/1/2012 the Volk "safe_align" branch mentioned in this blog post has been merged into the master branch on gnuradio.org. It will be a part of v3.5.2.